欧拉角三个角分别是什么坐标系，欧拉角的定义

很多朋友对于欧拉角三个角分别是什么坐标系和欧拉角的定义不太懂，今天就由小编来为大家分享，希望可以帮助到大家，下面一起来看看吧！

欧拉角是什么?

欧拉角是描述三维空间中刚体定位的关键角度参数，由章动角θ、旋进角ψ和自转角φ这三个独立的角参数组成。这个概念最早由欧拉提出，因此得名。

欧拉角是描述刚体在三维空间中取向的关键工具，通过三个有序的旋转角度来确定其相对于任意借鉴系的位置。不同的作者可能会采用不同的欧拉角组合和命名方式，因此在使用时需要明确定义。

欧拉角是描述三维空间中物体定向的角参数。它是一个完整的参数集，可以准确表示任何物体的旋转方向和姿态。下面详细解释欧拉角的概念。欧拉角包括多个参数，例如偏航角、俯仰角和滚转角等。这些角度参数描述了物体绕其三个主轴的旋转程度。在三维空间中，通过这三个角度的组合，可以唯一确定一个物体的方向。

欧拉角是用来确定定点转动刚体位置的3个一组独立角参量，由章动角θ、旋进角（即进动角）ψ和自转角j组成，因为欧拉首先提出而得名。

刚体(3):欧拉角、欧拉方程

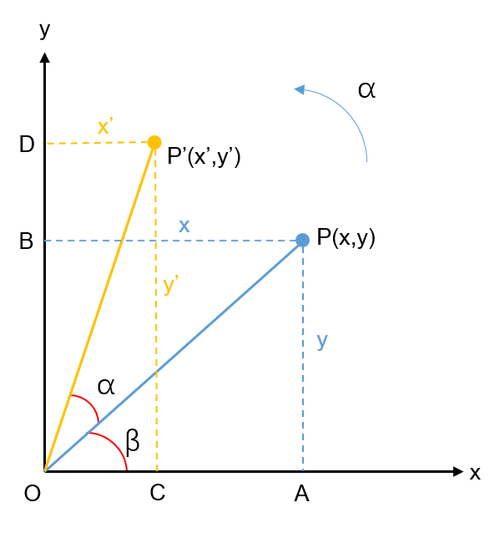
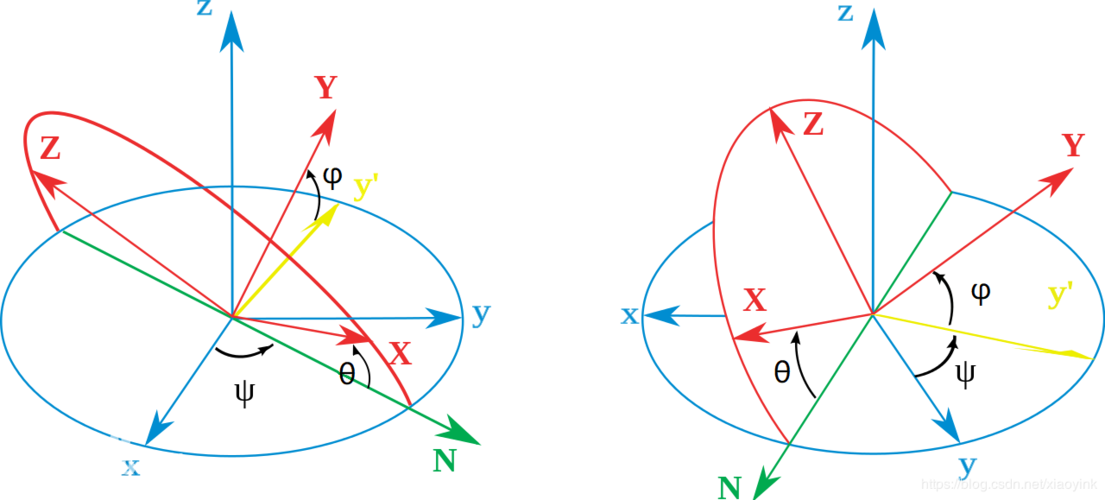
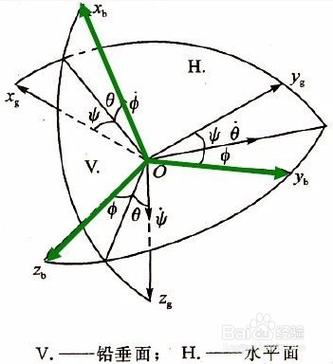
〖One〗、欧拉角是描述刚体动坐标系相对于固定坐标系空间取向的关键角度。通过三个特定的角，即Z轴与[公式]轴之间的夹角 [公式]，X轴与ON轴之间的夹角 [公式]，以及ON轴与 [公式]轴之间的夹角 [公式]，我们能完整地定义动坐标系的方位。

〖Two〗、刚体定点运动可用三个角度（称为欧拉角）的变化来描述；刚体定点转动时角速度变化和外力矩的关系；定点刚体在不受外力矩时的运动规律（称为定点运动的欧拉情况，这一成果1834年由L.潘索作出几何解释），以及自由刚体的运动微分方程等。

〖Three〗、欧拉角是描述物体三维旋转的参数，由欧拉首先提出，对于物理学中的热传导、振动和电磁波传播等问题，欧拉方程（ax^2D^2+bxD+c）y=f（x）是一个常见工具，它体现了二阶变系数线性微分方程的特征。

〖Four〗、数学家们把他的著作编成全集出版，竟达72卷之多。在欧拉的著作中，“无限小分析”方法是从欧拉开始的；变分学基础是欧拉方程；拓扑学中有欧拉数；刚体力学有欧拉角；复变函数中有欧拉函数；数论中有欧拉定理……后人称欧拉为“数学分析的化身”。在世界数学发展史上，人们把18世纪称为“欧拉时代”。

〖Five〗、就伦哈特·欧拉的情况而言，答案看来很明确：假如没有欧拉的公式、方程和方法，现代科学技术的进展就会滞后不前，实际上看来是不可想象的。

〖Six〗、欧拉数理化是指研究数学、物理和化学等自然科学领域中，与瑞士数学家欧拉（Leonhard Euler）相关的数学方法和理论体系。欧拉是18世纪最重要的数学家之一，他对数学的贡献广泛而深远，包括解析数论、复分析、微积分等领域。

偏航角【欧拉角】

〖One〗、导弹（或飞机）在空间中的方向通过三个角度来确定，即偏航角、俯仰角和滚转角。这三个角度，通常被称为欧拉角，或弹体的姿态角。偏航角、俯仰角和滚转角是描述弹体坐标系相对于地面坐标系的旋转角度。地面坐标系经过三次旋转，即可转到弹体坐标系。

〖Two〗、欧拉角是表示3D空间中任意旋转的三个数值。它包含三种类型：俯仰角（Pitch）、偏航角（Yaw）和滚转角（Roll）。以下图片展示了这三种角度：俯仰角表示我们向上或向下的视角，可以在第一张图中找到。第二张图展示了偏航角，它表示我们向左或向右看的程度。

〖Three〗、前面已经说过，确定导弹（或飞机）在空间中的方向需要用三个角度，分别为偏航角、俯仰角和滚转角，这三个角度通常称为欧拉角，或弹体的姿态角。这三个角度是地面坐标系与弹体坐标系之间的角度关系，即地面坐标系经过三次旋转即可转到弹体坐标系。

〖Four〗、欧拉角是描述三维空间中物体定向的角参数。它是一个完整的参数集，可以准确表示任何物体的旋转方向和姿态。下面详细解释欧拉角的概念。欧拉角包括多个参数，例如偏航角、俯仰角和滚转角等。这些角度参数描述了物体绕其三个主轴的旋转程度。在三维空间中，通过这三个角度的组合，可以唯一确定一个物体的方向。

〖Five〗、首先，欧拉角（横滚，俯仰，偏航）是相对地面而言的，所以对欧拉角求导也就是相对于地面坐标系而言。机体旋转角速率（通常用p，q，r表示）相对机体系本身的，他们之间存在着坐标系之间的变换。建模的时候一般都是认为四旋翼进行小角度飞行，所以此时机体角速度=欧拉角速度。

〖Six〗、欧拉角通常用于描述飞机或船舶等物体的旋转，例如，绕车头或机头方向的旋转角度被称为横滚角（roll），绕飞机顶部向上的轴旋转的角度被称为偏航角（yaw），绕飞机机身横向轴旋转的被称为俯仰角（pitch）。这种方式易于理解，但需要注意的是，欧拉角并非与xyz轴固定绑定，而是人为规定的。

欧拉角的基本概念

〖One〗、用一句话说，欧拉角就是物体绕坐标系三个坐标轴（x，y，z轴）的旋转角度。在这里，坐标系可以是世界坐标系，也可以是物体坐标系，旋转顺序也是任意的，可以是xyz，xzy，yxz，zxy，yzx，zyx中的任何一种，甚至可以是xyx，xyy，xzz，zxz等等等等。。所以说欧拉角多种多样。

〖Two〗、欧拉角是描述三维空间中刚体定位的关键角度参数，由章动角θ、旋进角ψ和自转角φ这三个独立的角参数组成。这个概念最早由欧拉提出，因此得名。

〖Three〗、欧拉角是描述三维空间中物体定向的角参数。它是一个完整的参数集，可以准确表示任何物体的旋转方向和姿态。下面详细解释欧拉角的概念。欧拉角包括多个参数，例如偏航角、俯仰角和滚转角等。这些角度参数描述了物体绕其三个主轴的旋转程度。在三维空间中，通过这三个角度的组合，可以唯一确定一个物体的方向。

〖Four〗、首先，欧拉角的定义是基于三个轴（X、Y、Z）的旋转，其中roll对应X轴，pitch对应Y轴，yaw对应Z轴，每个轴的旋转范围是（-180°， +180°）。不同的旋转顺序会产生不同的姿态表示，例如有六种可能的顺序：（x-y-z， y-z-x， z-x-y， x-z-y， z-y-x， y-x-z）。

〖Five〗、欧拉角是表示3D空间中任意旋转的三个数值。它包含三种类型：俯仰角（Pitch）、偏航角（Yaw）和滚转角（Roll）。以下图片展示了这三种角度：俯仰角表示我们向上或向下的视角，可以在第一张图中找到。第二张图展示了偏航角，它表示我们向左或向右看的程度。

〖Six〗、欧拉角就是个概念，它把一个转动分解成三个方向的转动，可以用三个欧拉角表示一个转动R（θ1，θ2，θ3）。其中的θ1，θ2，θ3就是普通的角度，欧拉角用来确定定点转动刚体位置的3个一组独立角参量，由章动角θ、旋进角（即进动角）ψ和自转角j组成，为欧拉首先提出而得名。

滚转角的欧拉角

〖One〗、在描述飞行器或导弹在三维空间中的运动状态时，我们需要考虑三个关键角度，它们构成了弹体姿态的核心要素，被统称为欧拉角，或者弹体的姿态角。这三个角度包括偏航角、俯仰角和滚转角，它们共同决定了设备的方向和姿态。这些角度的定义是基于两个坐标系之间的关系，即地面坐标系与弹体坐标系之间的转换。

〖Two〗、前面已经说过，确定导弹（或飞机）在空间中的方向需要用三个角度，分别为偏航角、俯仰角和滚转角，这三个角度通常称为欧拉角，或弹体的姿态角。这三个角度是地面坐标系与弹体坐标系之间的角度关系，即地面坐标系经过三次旋转即可转到弹体坐标系。

〖Three〗、欧拉角是表示3D空间中任意旋转的三个数值。它包含三种类型：俯仰角（Pitch）、偏航角（Yaw）和滚转角（Roll）。以下图片展示了这三种角度：俯仰角表示我们向上或向下的视角，可以在第一张图中找到。第二张图展示了偏航角，它表示我们向左或向右看的程度。

欧拉角欧拉角

欧拉角可以用来表示刚体相对于固定坐标系的运动学方程，其中包含了章动角、进动角和自转角以及它们的微分。例如，当刚体绕通过定点O的轴线以角速度ω旋转时，其在动坐标系中的角速度分量可以用欧拉角及其微分表示。欧拉角在物理学、工程学和计算机图形学等领域有着广泛的应用。

欧拉角是描述刚体动坐标系相对于固定坐标系空间取向的关键角度。通过三个特定的角，即Z轴与[公式]轴之间的夹角 [公式]，X轴与ON轴之间的夹角 [公式]，以及ON轴与 [公式]轴之间的夹角 [公式]，我们能完整地定义动坐标系的方位。

一般更常叫做——欧拉角的“奇异点”。理解如下：『1』如果你大学以上——欧拉角是描述刚体转动的三个轴角。奇异点就是无法确定转动方向的角度，或者说是对应无数种可能转动方向的特定角度。如果你初接触，你可以想象一个在北极的人，你让他向南走，他有无数个走法。那么北极就是他运动的奇异点。

欧拉角是描述三维空间中刚体定位的关键角度参数，由章动角θ、旋进角ψ和自转角φ这三个独立的角参数组成。这个概念最早由欧拉提出，因此得名。

欧拉角，作为唯一确定定点转动刚体位置的三个一组独立角参量，由章动角θ、旋进角ψ和自转角j组成，由欧拉首先提出而得名。这组角描述了刚体在三维欧几里得空间的取向。莱昂哈德·欧拉利用欧拉角来描述刚体在三维空间中的位置。对于任何借鉴系，刚体的取向通过按照顺序进行三个欧拉角的旋转来设定。

欧拉角是用三次独立的绕确定轴的旋转角度表示姿态的一种方法，通常在航空航天领域中使用。欧拉角由三次旋转构成：第一次绕z轴旋转一个角度（yaw），第二次绕旋转后的y轴旋转一个角度（pitch），第三次绕第二次旋转后的x轴旋转一个角度（roll）。

弹道导弹运动参数定义是什么?是在什么坐标系下定义的?

弹体坐标系与惯性坐标系形成三个欧拉角，即俯仰角，偏航角和滚转角；速度坐标系与弹体坐标系形成攻角与侧滑角；速度坐标系与惯性坐标系形成弹道倾角和航向角。

下定义。用简明的语言对某一概念的本质特征作规定性的说明叫下定义。下定义能准确揭示事物的本质，是科技说明文常用的方法。『7』作诠释。从一个侧面，就事物的某一个特点做些解释，这种方法叫诠释法。 。『8』打比方。

航母的战斗逻辑是用飞机直接把敌人消灭在距离航母数百公里之外的领域，没有一种舰载雷达的扫描范围能超过预警机，没有一种舰载反舰导弹的射程能超过飞机的航程，没有任何一种舰载反潜设备的反潜能力能超过反潜飞机或直升机，飞机就是比较好的进攻和防御武器，所以无需再安装其它进攻性武器。

欧拉角的解释

〖One〗、欧拉角是描述三维空间中物体定向的角参数。它是一个完整的参数集，可以准确表示任何物体的旋转方向和姿态。下面详细解释欧拉角的概念。欧拉角包括多个参数，例如偏航角、俯仰角和滚转角等。这些角度参数描述了物体绕其三个主轴的旋转程度。在三维空间中，通过这三个角度的组合，可以唯一确定一个物体的方向。

〖Two〗、欧拉角是用来唯一地确定定点转动明体位置的三个一组独立角参量，由章动角θ、进动角ψ和自转角φ组成，为L.欧拉首先提出，故得名。它们有多种取法，下面是常见的一种。如图所示，由定点O作出固定坐标系Oxyz以及固连于刚体的坐标系Oxyz。

〖Three〗、欧拉角：直观的旋转指南如同在成都街头寻找春熙路，欧拉角就像问路时的第二种它采用的是相对坐标系统，便于理解。欧拉角的算法思想就如同你询问方向时，先告诉你要绕着哪个方向旋转，再沿着自身轴线转动，最后再调整另一个轴。

〖Four〗、欧拉角用于三维空间中表示方向和方向变换，通过指定与三个旋转轴相关联的三个角度。欧拉角表示方法便于理解，但存在Ambiguity问题，即给定欧拉角可能对应多个方向。为解决此问题，引入轴角表示和四元数。轴角表示使用旋转轴和旋转角度唯一表示方向，避免了Ambiguity。

〖Five〗、欧拉角则是指绕坐标系三个轴（x、y、z轴）的旋转角度，旋转顺序与坐标系统相关，最常见的是Roll-Pitch-Yaw（或x-y-z）方式表示。这方法利在直观且易理解，但存在万向节死锁问题，即在某些特定旋转组合后，后续旋转方向受限。

〖Six〗、欧拉角 中文名称：欧拉角 英文名称：Euler angles 定义：构件在三维空间中的有限转动，可依次用三个相对转角表示，即进动角、章动角和自旋角，这三个转角统称为欧拉角。欧拉角用来确定定点转动刚体位置的3个一组独立角参量，由章动角θ、旋进角（即进动角）ψ和自转角j组成，为欧拉首先提出而得名。

欧拉角三个角分别是什么坐标系和欧拉角的定义的问题分享结束啦，以上的文章解决了您的问题吗？欢迎您下次再来哦！